A Condição De Alinhamento De Três Pontos Exemplos é um conceito fundamental em geometria, com aplicações práticas em vários campos. Neste artigo, exploraremos exemplos específicos dessa condição, suas implicações geométricas e métodos para verificar o alinhamento de três pontos.
Vamos mergulhar no fascinante mundo da Condição De Alinhamento De Três Pontos Exemplos e descobrir seus usos práticos no mundo real.
Exemplos de Condição de Alinhamento de Três Pontos

Condição de alinhamento de três pontos é uma propriedade geométrica que ocorre quando três pontos distintos estão localizados em uma linha reta. Existem vários exemplos dessa condição em diferentes contextos, incluindo geometria, física e engenharia.
Em geometria, a condição de alinhamento de três pontos pode ser determinada usando métodos geométricos, como medição de distâncias e ângulos. Por exemplo, se três pontos A, B e C formam um triângulo, eles estão alinhados se a soma dos comprimentos de quaisquer dois lados for maior que o comprimento do terceiro lado.
Exemplo 1: Colinearidade em Física
Em física, a condição de alinhamento de três pontos é essencial para analisar o movimento de objetos. Por exemplo, quando uma partícula se move ao longo de uma linha reta, sua trajetória pode ser representada por uma equação linear. Os coeficientes desta equação determinam a inclinação e o intercepto da linha, que representam o deslocamento e a velocidade da partícula, respectivamente.
Aplicações Práticas da Condição de Alinhamento de Três Pontos: Condição De Alinhamento De Três Pontos Exemplos

A condição de alinhamento de três pontos é uma ferramenta valiosa em vários campos, como engenharia, arquitetura e física. Ela permite que os profissionais determinem se três pontos estão alinhados e, portanto, ajuda na resolução de problemas e no projeto de estruturas.
Na engenharia, a condição de alinhamento de três pontos é usada para verificar o alinhamento de componentes em máquinas e estruturas. Por exemplo, em um motor de combustão interna, a condição de alinhamento de três pontos é usada para verificar o alinhamento do virabrequim, bielas e pistões.
Na arquitetura, a condição de alinhamento de três pontos é usada para verificar o alinhamento de paredes, pisos e tetos. Isso é importante para garantir que a estrutura seja estável e segura.
Na física, a condição de alinhamento de três pontos é usada para determinar se três forças estão em equilíbrio. Isso é importante para analisar o movimento de objetos e projetar estruturas.
Exemplo de Engenharia, Condição De Alinhamento De Três Pontos Exemplos
Em um motor de combustão interna, o virabrequim, as bielas e os pistões devem estar alinhados para que o motor funcione corretamente. A condição de alinhamento de três pontos é usada para verificar se esses componentes estão alinhados. Se os componentes não estiverem alinhados, o motor pode sofrer danos.
Exemplo de Arquitetura
Em um edifício, as paredes, pisos e tetos devem estar alinhados para que a estrutura seja estável e segura. A condição de alinhamento de três pontos é usada para verificar se esses componentes estão alinhados. Se os componentes não estiverem alinhados, a estrutura pode sofrer danos ou mesmo desabar.
Métodos para Verificar a Condição de Alinhamento de Três Pontos

Para determinar se três pontos estão alinhados, existem métodos analíticos e geométricos. Esses métodos oferecem abordagens distintas para verificar o alinhamento, com vantagens e desvantagens específicas.
Métodos Analíticos
Os métodos analíticos utilizam equações matemáticas para verificar o alinhamento. Eles são precisos e podem ser aplicados a pontos em qualquer dimensão.
- Método do Determinante:Calcula o determinante de uma matriz formada pelas coordenadas dos pontos. Se o determinante for zero, os pontos estão alinhados.
- Método da Área:Calcula a área do triângulo formado pelos três pontos. Se a área for zero, os pontos estão alinhados.
Métodos Geométricos
Os métodos geométricos utilizam propriedades geométricas para verificar o alinhamento. Eles são visualmente intuitivos e fáceis de aplicar, mas podem ser menos precisos do que os métodos analíticos.
- Método da Linha Reta:Desenha-se uma linha reta que passa por dois dos pontos. Se o terceiro ponto estiver na linha, os pontos estão alinhados.
- Método do Ângulo:Mede-se o ângulo entre os vetores formados pelos pares de pontos. Se todos os ângulos forem iguais a 180 graus, os pontos estão alinhados.
Tabela Comparativa de Métodos
| Método | Vantagens | Desvantagens |
|---|---|---|
| Determinante | Preciso, aplicável a qualquer dimensão | Complexidade computacional |
| Área | Simples, intuitivo | Menos preciso, pode falhar para pontos colineares |
| Linha Reta | Visualmente intuitivo, fácil de aplicar | Menos preciso, pode ser afetado por erros de desenho |
| Ângulo | Intuitivo, fácil de medir | Menos preciso, pode ser afetado por erros de medição |
Implicações Geométricas da Condição de Alinhamento de Três Pontos

A condição de alinhamento de três pontos tem profundas implicações geométricas, fornecendo informações valiosas sobre as relações entre os pontos e as linhas que os conectam.
Essas implicações podem ser usadas para resolver problemas geométricos, determinar as propriedades das figuras e estabelecer relacionamentos entre diferentes elementos geométricos.
Colinearidade
Quando três pontos estão alinhados, eles são colineares, ou seja, eles estão localizados em uma mesma linha reta. Isso implica que a distância entre quaisquer dois pontos da linha é igual à soma das distâncias entre os pontos e o terceiro ponto.
A colinearidade é uma propriedade importante para identificar linhas paralelas e perpendiculares, pois linhas paralelas nunca se cruzam e linhas perpendiculares se cruzam em ângulos retos.
Paralelismo
Se dois pontos estão alinhados com um terceiro ponto, eles são paralelos entre si. Isso implica que as linhas que passam pelos pontos paralelos nunca se cruzam, independentemente da distância entre eles.
O paralelismo é uma propriedade fundamental para construir figuras simétricas e determinar as proporções entre diferentes segmentos de linha.
Perpendicularidade
Quando um ponto está alinhado com dois outros pontos, ele é perpendicular à linha que os conecta. Isso implica que o ângulo formado entre a linha e o segmento de linha que conecta o ponto perpendicular é de 90 graus.
A perpendicularidade é essencial para criar figuras geométricas precisas, como quadrados e retângulos, e para determinar as distâncias entre pontos e linhas.
Extensões da Condição de Alinhamento de Três Pontos
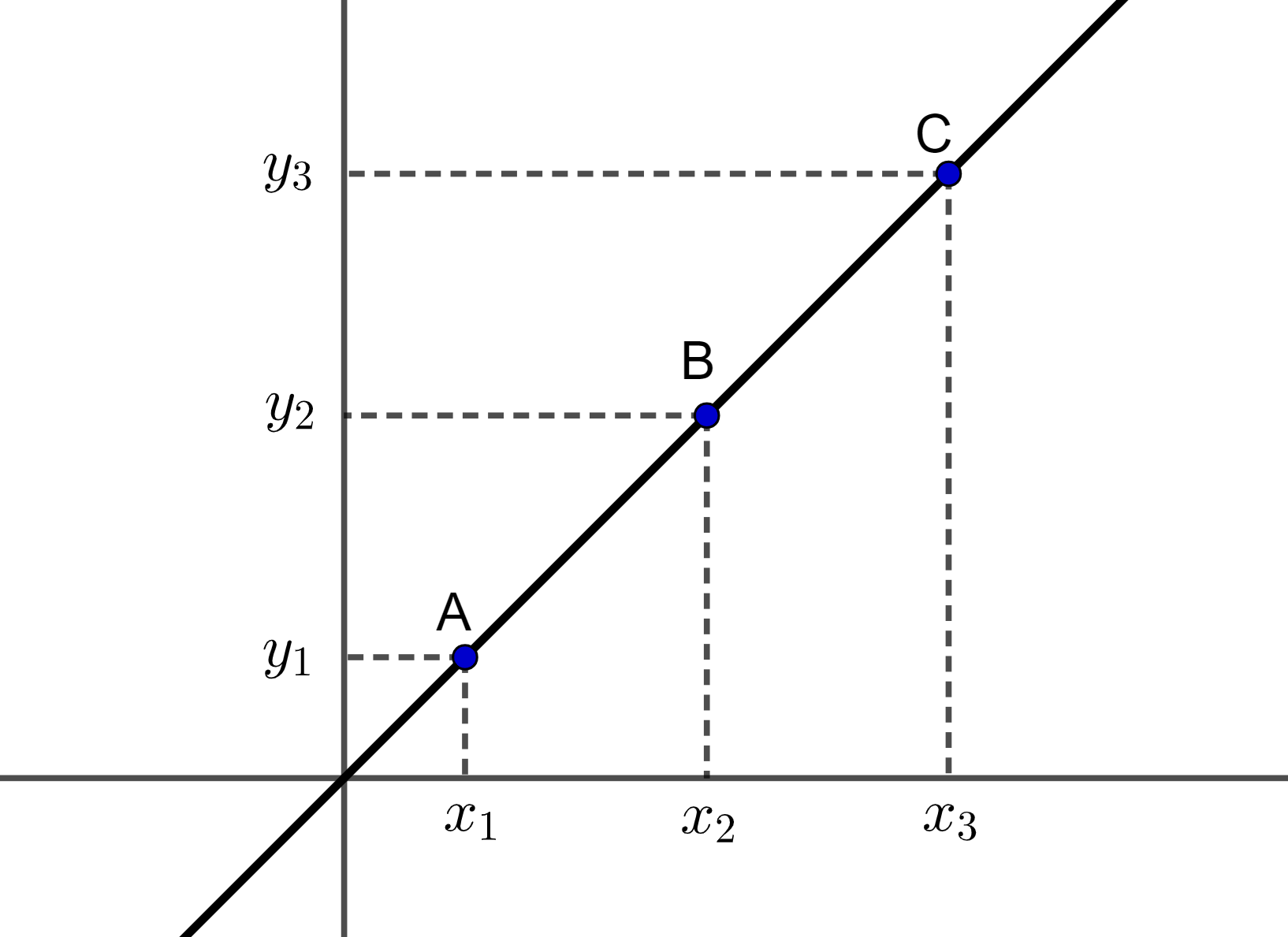
A condição de alinhamento de três pontos pode ser estendida para mais de três pontos, permitindo o alinhamento de quatro, cinco ou mais pontos.
Essas extensões são úteis em vários contextos, como verificação de paralelismo de linhas, alinhamento de máquinas e calibração de instrumentos.
Alinhamento de Quatro Pontos
A extensão da condição de alinhamento de três pontos para quatro pontos envolve a verificação da colinearidade de três pares de pontos. Se todos os três pares forem colineares, então os quatro pontos estão alinhados.
Esta extensão é particularmente útil para verificar o paralelismo de linhas, pois permite determinar se quatro pontos estão localizados em linhas paralelas.
Alinhamento de Cinco Pontos
A extensão da condição de alinhamento de três pontos para cinco pontos envolve a verificação da colinearidade de quatro pares de pontos. Se todos os quatro pares forem colineares, então os cinco pontos estão alinhados.
Esta extensão é útil para verificar o alinhamento de máquinas e equipamentos, pois permite determinar se cinco pontos estão localizados em uma linha reta.
Limitações
Embora as extensões da condição de alinhamento de três pontos sejam úteis, elas também têm algumas limitações. Essas extensões só podem ser aplicadas a pontos que estão no mesmo plano. Além disso, a precisão das extensões depende da precisão das medições dos pontos.
Em resumo, a Condição De Alinhamento De Três Pontos Exemplos é uma ferramenta poderosa para analisar e resolver problemas geométricos. Suas aplicações práticas em engenharia, arquitetura e física destacam sua importância no mundo real. Ao compreender as implicações geométricas e os métodos de verificação, podemos aproveitar totalmente os benefícios dessa condição para projetar estruturas estáveis e resolver problemas geométricos complexos.

